| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 데이터 분석
- input
- scikit-learn
- 파이썬
- pandas
- selenium
- 데이터분석
- 인공지능
- Udemy
- SQL
- 태블로
- numpy
- Okt
- Word Cloud
- 시각화
- 크롤링
- 형태소분석기
- ionehotencoding
- pyspark
- iNT
- Python
- Tableau
- 데이터
- 머신러닝
- konlpy
- Today
- Total
반전공자
R - Outlier 찾아내기 본문
예제) 멀리뛰기
뛴 지점(마지노선에서 얼마나 떨어져 있는가/ avg_takgeoff) 이 짧아질수록 뛴 거리(best_jump)가 길 것이라고 기대한다.
best_jump = c(5.30, 5.55, 5.47, 5.45, 5.07, 5.32, 6.15, 4.70, 5.22,
5.77, 5.12, 5.77, 6.22, 5.82, 5.15, 4.92, 5.20, 5.42)
avg_takeoff = c(.09, .17, .19, .24, .16, .22, .09, .12, .09,
.09, .13, .16, .03, .50, .13, .04, .07, .04)임의의 값을 집어넣어 준다.
plot(avg_takeoff, best_jump)
jump_model = lm(best_jump~avg_takeoff)
abline(reg = jump_model, col = "red")그래프를 그리고, best_jump와 avg_takeoff 간의 선형관계를 lm 함수를 통해 jump_model에 저장
그려놓았던 그래프에 선형모델을 덧그린다.

summary(jump_model)
< lm 해석 >
Intercept의 Estimate는 절편을, avg_takeoff의 Estimate는 기울기를 나타낸다.
avg_takeoff의 Estimate 값이 양수이기 때문에 우상향하는 그래프를 그리고 있다.
avg_takeoff의 Pr 값이 0.05보다 크기 때문에 설명변수 없이 선형모델을 낸 것이 더 의미가 있다고 보여진다.
마지막 줄의 p-value가 0.05보다 크기 때문에 별 의미가 없고, Adjusted R-squaerd의 값은 높을수록 모델이 데이터를 잘 설명한다고 볼 수 있는데, 위의 값은 -0.04이기 때문에 설명을 못하는 모델이라는 것을 알 수 있다.
< 그래프 해석 >
우리가 생각한 가정은, takeoff가 짧아질수록 best_jump가 길어진다. 였는데,
그래프는 반대라고 말하고 있다.
takeoff가 길어질수록 best_jump가 길어진다?
그래프를 살펴보니, 혼자만 동떨어져있는 데이터가 보인다.
정말 저 포인트가 Outlier인지 알아보자.
plot(jump_model)
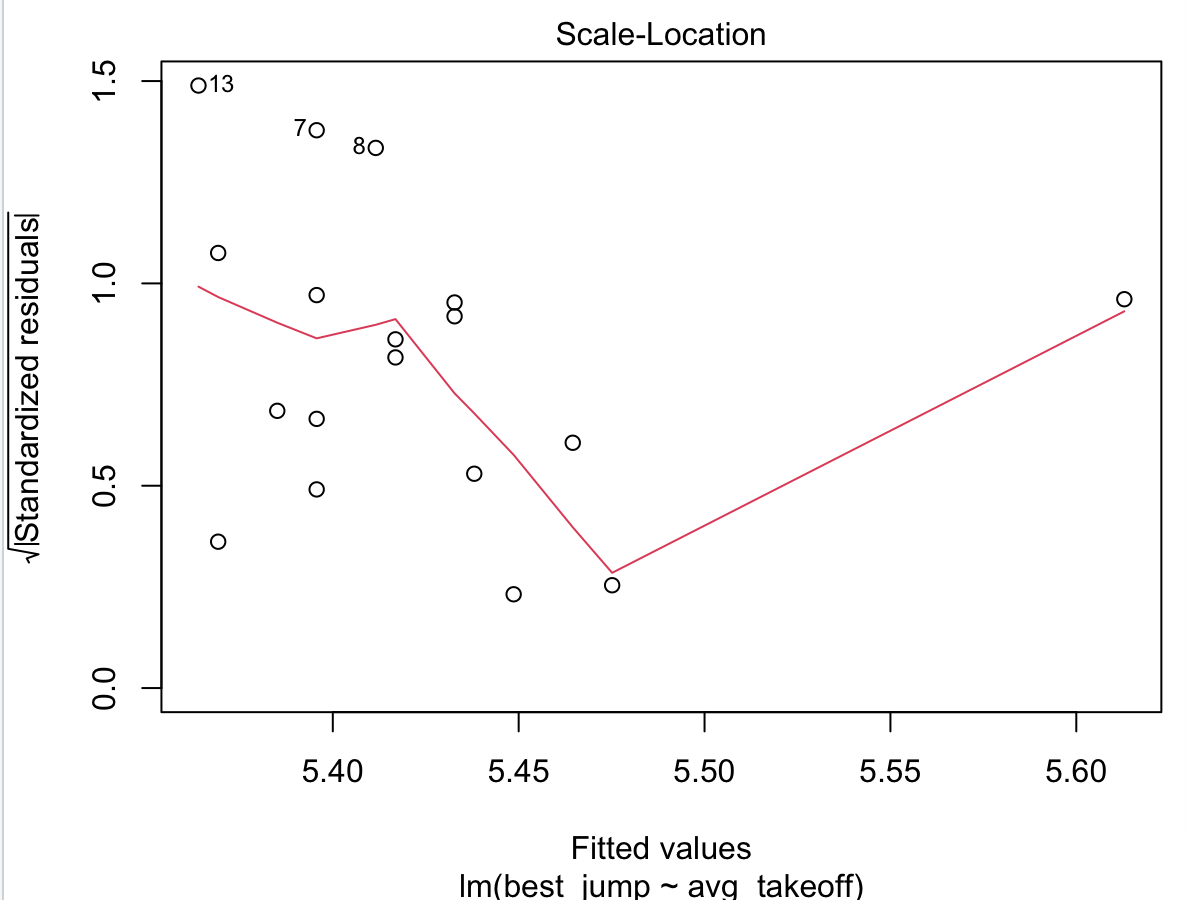

첫번째 그래프 - 가운데의 기준선인 '0'에 가까운 것이 가장 이상적이지만 특별한 양상을 보이고 있기 때문에 좋지 않다.
두번째 그래프 - 갑자기 위로 치솟는 양상을 보이고 있음은 특이한 패턴이기 때문에 이상하다고 보여진다.
세번째 그래프 - 가에 그려져있는 쿡의 거리에 14 데이터가 거진 넘어가 있는 상태이다. 이는 웬만하면 일어나지 않는 데이터로 "이상치" 라고 보여진다.
▶ Outlier를 제거하고 선형회귀모델을 만들어야 타당할 것이다.
< Outlier 제거 >
n_best_jump = best_jump[-14]
n_avg_takeoff = avg_takeoff[-14]이상치인 14번 데이터를 best_jump, avg_takeoff에서 제거한다.
< 모델 재 제작 >
jump_model2 = lm(n_best_jump~n_avg_takeoff)Outlier를 제거한 데이터로 다시 선형 회귀 모델을 제작한다.
summary(jump_model2)
아까와 다르게 n_avg_takeoff의 Estimate 값이 음수로 바뀌었다.
이는 그래프가 우하향하는 그래프의 양상으로 변했다는 것을 보이고,
두 모델의 차이점은 "이상치 제거"이기 때문에 이상치 하나가 그래프의 기울기에 큰 영향을 미치고 있었다는 것을 알 수 있었다.
'데이터분석 > R' 카테고리의 다른 글
| R - 단순선형회귀 실습 (키와 몸무게 관계 분석) (0) | 2021.06.15 |
|---|---|
| R - < 회귀분석 > (0) | 2021.06.15 |
| R 데이터 분석 프로젝트 - Titanic (Decision tree) (0) | 2021.06.09 |
| R # airquality - 선형회귀모델 (0) | 2021.05.27 |
| R - ANOVA(아노바) / PlantGrowth (ANOVA, Tukey HSD) (0) | 2021.05.23 |

