| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- pandas
- input
- pyspark
- ionehotencoding
- 인공지능
- Tableau
- numpy
- selenium
- Okt
- 태블로
- SQL
- 데이터 분석
- 데이터
- 형태소분석기
- 데이터분석
- 크롤링
- iNT
- scikit-learn
- Python
- konlpy
- Udemy
- 머신러닝
- 시각화
- Word Cloud
- 파이썬
- Today
- Total
반전공자
R - 단순선형회귀 실습 (키와 몸무게 관계 분석) 본문
< 분석 단계 >
①. 데이터 특성 파악 : 산점도, boxplot ..
②. 키와 몸무게 사이의 상관관계 확인 : cor.test()
③. 선형회귀모델 생성 : lm()
④. 검증 : summary(), plot()
⑤. 예측 : predict()
dataset: regression.csv
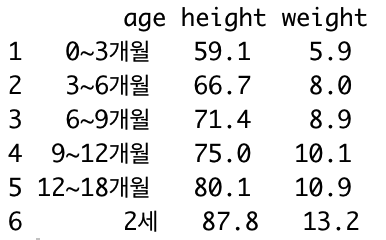
① 데이터 불러오기, 특성 파악
reg = read.csv("regression.csv")
head(reg)
plot(reg$weight, reg$height)

우상향하는 경향을 보인다.
②. 상관관계 확인
cor(reg$height, reg$weight)
cor.test(reg$height, reg$weight)→ cor, cor.test 둘 중 아무거나 써도 상관 없음.
cor()은 상관계수만 보여준다.
cor.test가 더 상세한 수치들을 보여준다.

상관계수 (cor) = 0.9672103
▶ 강한 양적 선형관계를 가진다. (1에 가깝기 때문)
③. 선형회귀모델 생성
r = lm(reg$height~reg$weight)
abline(r, col = "red")
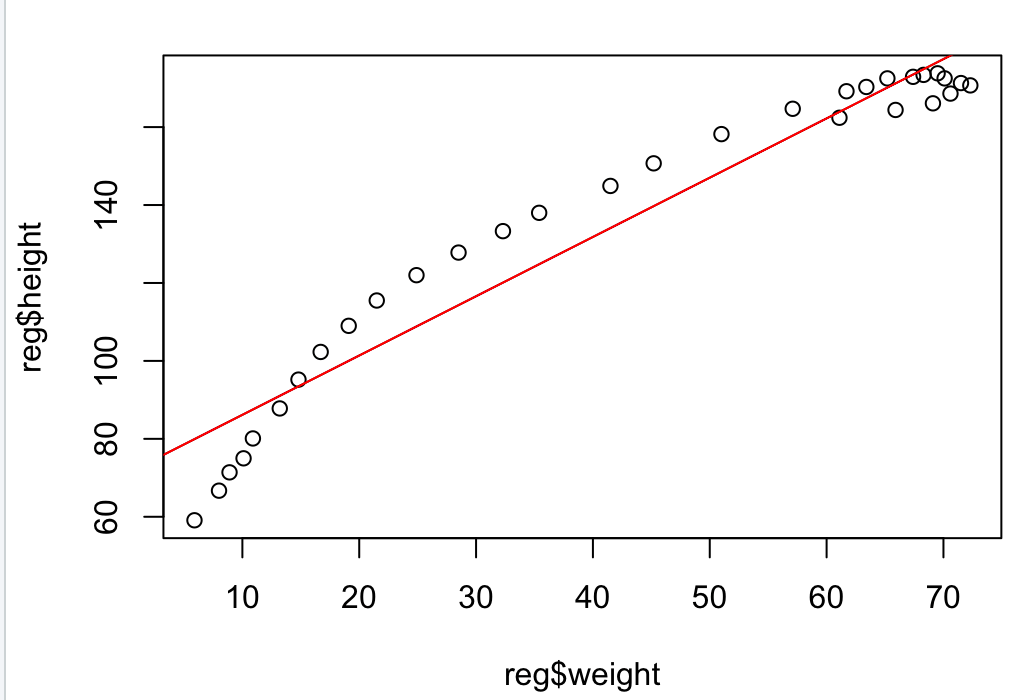
이전에 그렸던 그래프에 회귀선 추가
④ 검증
summary(r)
Coefficients (선형회귀모델계수)
: Pr 값의 우측에 ***이 표시되어 있음 = 유의미한 값이다.
Intercept(y 절편) + reg$weight(기울기) * x = 회귀선
☞ 70.9481 + 1.5218 * x
Multiple R-squared
→ 회귀선이 데이터의 약 93%를 설명한다.
Adjusted R-squared
→ 다른 독립변수를 추가해도 어느 정도 맞게해주는 값 (위 예시에서는 약 93%의 정확도)
p-value < 0.05
→ reg$height의 coefficient가 통계적으로 유의미함.
plot(r)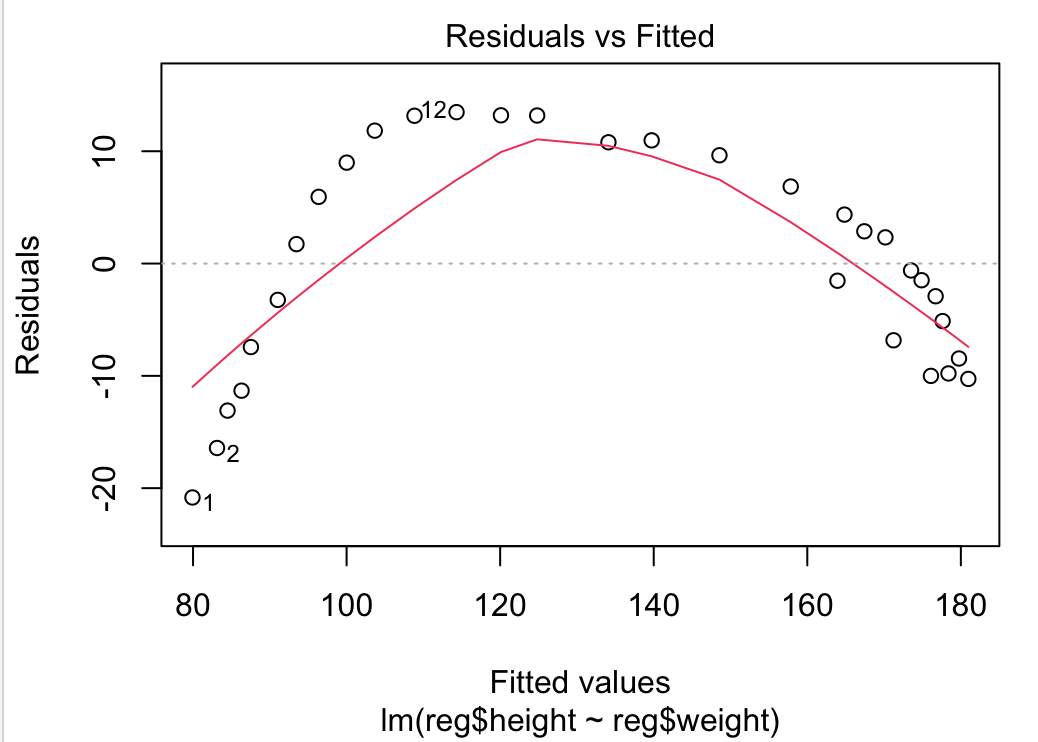



①번째 그래프
x축 = 선형회귀로 예측된 Y 값 / y축 = 잔차(Residual)
기울기 0인 경우가 가장 이상적
②번째 그래프
잔차가 정규분포를 따르는지 확인
③번째 그래프
x축 = 선형회귀로 예측된 Y 값 / y축 = 표준화된 잔차
기울기 0인 경우가 가장 이상적
④번째 그래프
x축 = 레버리지 / y축 = 표준화된 잔차
레버리지 : 설명 변수가 얼마나 극단에 치우쳐져있는지에 대한 정도
Cook's distance : 크게 벗어나있는 데이터를 판별하는 선
'데이터분석 > R' 카테고리의 다른 글
| R - [실습: ANOVA(감기약, 피로도) ] 미완글 (0) | 2021.06.21 |
|---|---|
| R - < 회귀분석 > (0) | 2021.06.15 |
| R - Outlier 찾아내기 (0) | 2021.06.11 |
| R 데이터 분석 프로젝트 - Titanic (Decision tree) (0) | 2021.06.09 |
| R # airquality - 선형회귀모델 (0) | 2021.05.27 |

