| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 데이터 분석
- pandas
- 태블로
- 파이썬
- SQL
- selenium
- 인공지능
- ionehotencoding
- input
- 머신러닝
- 데이터분석
- numpy
- Okt
- 데이터
- Python
- konlpy
- 시각화
- Tableau
- 형태소분석기
- iNT
- Word Cloud
- scikit-learn
- Udemy
- pyspark
- 크롤링
- Today
- Total
반전공자
R - 분석방법 (카이제곱, 피셔검정, KS검정, Shapiro 검정, t-test) 본문
[ 카이제곱 검정 - chisq.test() ]
# 독립성 검정 : 두 명목 변수 사이에 관계가 있는지 확인
# 적합도 검정 : 관측 결과가 특정한 분포로부터의 관측값인지 검정 ex. 실험 결과가 이론과 일치하는가, 어긋나는가?
# 동질성 검정 : 두 집단의 분포가 동일한지 검정 ex. 남, 여학생의 국,영,수 선호도가 같은가 다른가?
- H0(귀무가설) : 두 명목변수는 독립이다. ( p > 0.05 )
- H1(대립가설) : 두 명목변수는 독립이 아니다. ( p < 0.05 )
library(MASS)
data("survey")
str(survey)
SexExer = xtabs(~Sex+Exer, data=survey)
chisq.test(SexExer)


* df(자유도) : (2-1)*(3-1) = (성별레벨-1)*(운동레벨-1) = 2
>> p-value 가 0.05보다 크기 때문에 귀무가설을 기각할 수 없다.
[ 성별과 운동은 독립이다. ]
[ 피셔검정 - fisher.test() ]
# 표본수가 적거나, 분할표가 치우치게 분포된 경우에 적용
- H0(귀무가설) : 관련(차이) 없다. ( p > 0.05)
- H1(대립가설) : 관련(차이) 있다. (p < 0.05)
Q. child1, child2의 장난감 비율의 차이가 있는가?
child1 <- c(5, 11, 1)
child2 <- c(4, 7, 3)
Toy <- cbind(child1, child2)
rownames(Toy) <- c("car", "truck", "doll")
fisher.test(Toy)
>> p-value가 0.05보다 크기 때문에 귀무가설을 기각할 수 없다.
[ 비율 차이 없다. ]
카이제곱검정을 실행하면?
chisq.test(Toy)

>> 역시 p-value가 0.05보다 크기 때문에 귀무가설을 기각할 수 없다.
[ 비율 차이 없다. ]
but, warning message가 뜬다.

→ fisher.test()를 수행해야 함.
그래프로 그려보면?
plot(x, dchisq(x,2), type="l")
[ KS 검정 - ks.test() ]
# 데이터의 누적 분포 함수와 비교하고자 하는 누적분포 함수 간의 최대 거리를 통계량으로 사용하여 가설 검정
x <- rnorm(50)
y <- runif(30)
ks.test(x,y)
>> p-value가 0.05보다 작으므로 귀무가설을 기각하고 대립가설을 채택한다.
[ 분포가 같지 않다. (차이가 존재한다) ]
[ Shapiro Wilk Test - shapiro.test() ]
# 데이터가 정규분포를 따르는지 검정
- H0(귀무가설) : 정규분포이다. ( p > 0.05)
- H1(대립가설) : 정규분포가 아니다. (p < 0.05)
shapiro.test(rnorm(100, mean=5, sd=3))
>> p-value가 0.05보다 크므로, 귀무가설을 기각할 수 없다.
[ 정규분포를 따른다. ]
정규분포가 아닌 값을 넣어서 정규분포를 하는지 검정해보자.
shapiro.test(runif(100, min=2, max=4))

>> p-value가 0.05보다 작기 때문에 귀무가설을 기각하고 대립가설을 채택해야 한다.
[ 정규분포를 따르지 않는다. ]
** 통계량에 의한 정규성 검정 : shapiro.test()
** 그래프에 의한 정규성 검정 : Histogram, Q-Q plot
[ 실습: 단일 모집단 분포의 정규성 검정 ] - cfb::UsingR
Q. Customer의 INCOME 분포는 정규성을 보이는가?
install.packages("UsingR")
library(UsingR)
str(cfb)
shapiro.test(cfb$INCOME)
hist(cfb$INCOME, breaks = 100)
hist(cfb$INCOME, freq=FALSE, breaks = 100,
main="Kernel Density Plot of cfb$INCOME")
# freq = FALSE 면 데이터의 확률 밀도를 그린다.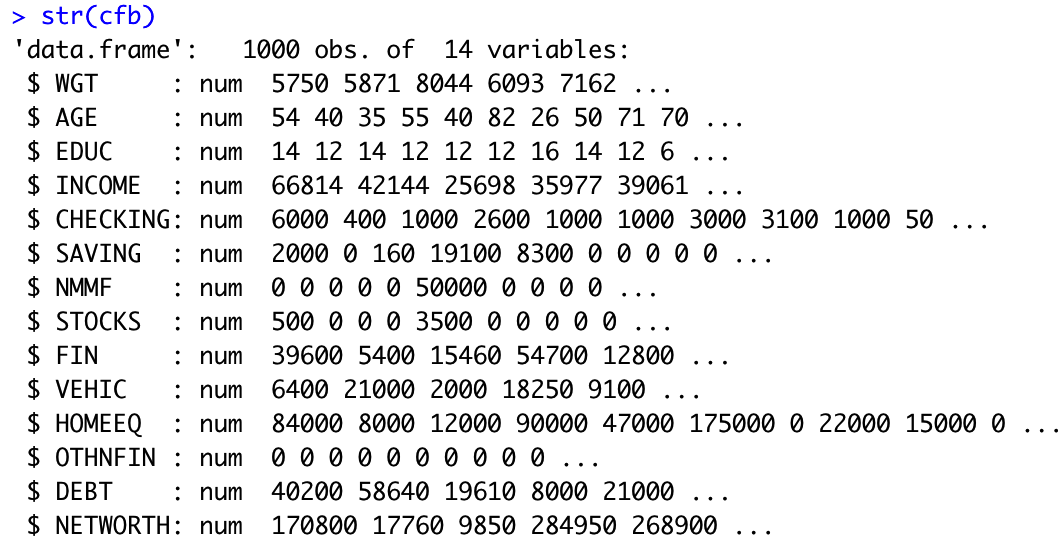

>> p-value가 0.05보다 훨씬 작은 값이기 때문에 귀무가설을 기각하고 대립가설을 채택해야 한다.
[ 정규성을 보이지 않는다. ]
[ Histogram ]
그래프로 나타내볼까?


[ Q-Q plot ]
qqnorm(cfb$INCOME)
qqline(cfb$INCOME)
>> 데이터가 직선 위에 있어야 하는데 직선관계가 아니다.
[ 정규분포를 하지 않는다. ]
[ T - test _ t.test() ]
# 하나 또는 두 개 집단의 평균을 비교하는 Parametric Test (모수적 감정법)
# 조건 :
- 측정값이 정규분포를 한다.
- 평균이 그 집단의 대표값 역할을 수행하는 경우
# 표본이 하나
# 표본이 둘
- 독립된 두 집단의 경우 : Two-sample t-test
- 관련된 두 집단의 경우 : Paired t-test (짝지어진 값들 간 차이 구한 후, 차이 값들의 평균이 0인지 검정)
- if, 두 집단의 분산이 동일하지 않다면 Smith/WelchSatterthwaite test
** t-test는 분산이 동일한 것을 가정한다.
# 정규분포를 하지 않는 경우 (=비모수적 검정)
- Two-sample t-test 대신 Wilcoxon rank sum test(Mann-Whitney U test)
- Paired t-test 대신 Wilcoxon signed rank test
* t-test를 수행하기 전에 분석의 대상이 되는 데이터가 정규분포를 하는지 검증 필요 (shapiro.test())
[ 사례 1 ]
회사 건전지 수명이 1000시간일 때, 무작위로 뽑은 10개의 건전지에 대한 수명이 아래의 값,
샘플이 모집단과 다르다고 할 수 있나?
a <- c(980, 1008, 968, 1032, 1012, 996, 1021, 1002, 996, 1017)
shapiro.test(a)
>> p-value가 0.05보다 크기 때문에 귀무가설을 기각할 수 없다.
[ 정규분포를 따른다. ]
** 정규분포를 따르기 때문에 t-test를 수행할 수 있다.
t.test(a, mu=1000, alternative = "two.sided")
# mu: 비교 대상의 평균
# alternative: "다르다"를 보기 때문에 two.sided
# default값이 two.sidedH0(귀무가설) : 같다. (모집단의 평균이 1000시간이다.)
H1(대립가설) : 다르다

>> p-value가 0.05보다 크기 때문에 귀무가설을 기각할 수 없다.
[ 같다. 모집단의 평균이 1000시간이다. ]
[ 사례 2 ]
Q. 평균 성적이 55점, 0교시 수업 이후의 성적은 아래와 같고, 0교시 수업 시행 이후의 학생들의 성적이 올랐다고 할 수 있을까?
b <- c(58, 49, 39, 99, 32, 88, 62, 30, 55, 65, 44, 55, 57, 53, 88, 42, 39)
shapiro.test(b)** 데이터의 개수가 30개 이하이면, 정규분포를 따르는지 검사해야 한다.

>> p-value가 0.05보다 크기 때문에 귀무가설을 기각할 수 없다.
[ 정규분포를 따른다. ]
→ 정규분포를 따르기 때문에 t-test를 수행할 수 있다.
t.test(b, mu=55, alternative = "greater")
# 올랐는가, 혹은 같거나 떨어졌느냐를 증명하는 것이기 때문에 alternative="greater"
>> p-value가 0.05 보다 크기 때문에 귀무가설을 기각할 수 없다.
H0(귀무가설) : 오르지 않았다. (모집단의 평균이 55점이다.)
H1(대립가설) : 올랐다.
[ 성적이 오르지 않았다. ]
[ 사례 3 ] : 표본이 두 개인 경우
환자 10명을 상대로 혈압약을 먹지 않을 때와 먹었을 때의 혈압을 측정하고 이 두 자료의 평균이 다르다고 할 수 있는지 검증해라.
pre = c(13.2, 8.2, 10.9, 14.3, 10.7, 6.6, 9.5, 10.8, 8.8, 13.3)
post = c(14.0, 8.8, 11.2, 14.2, 11.8, 6.4, 9.8, 11.3, 9.3, 13.6)
shapiro.test(pre)
shapiro.test(post)
>> p-value가 0.05보다 크기 때문에 귀무가설을 기각할 수 없다.
[ 정규분포를 따른다. ]

>> p-value가 0.05보다 크기 때문에 귀무가설을 기각할 수 없다.
[ 정규분포를 따른다. ]
* 두 집단 모두 정규분포를 따르기 때문에 t-test를 수행할 수 있다.
t.test(pre, post)
H0(귀무가설) : 차이가 없다. (평균이 같다.)
H1(대립가설) : 차이가 있다.
>> p-value가 0.05보다 크기 때문에 귀무가설을 기각할 수 없다.
[ 평균이 같다. ]
var.test(pre,post)# pre, post가 같은 분산을 가지나?
>> p-value가 0.05보다 크기 때문에 귀무가설을 기각할 수 없다.
[ 같은 분산을 가진다. ]
t.test(pre,post, paired = FALSE, var.equal = TRUE)
# paired = FALSE : 짝지어지지 않음.
# var.equal = TRUE : 분산이 같다.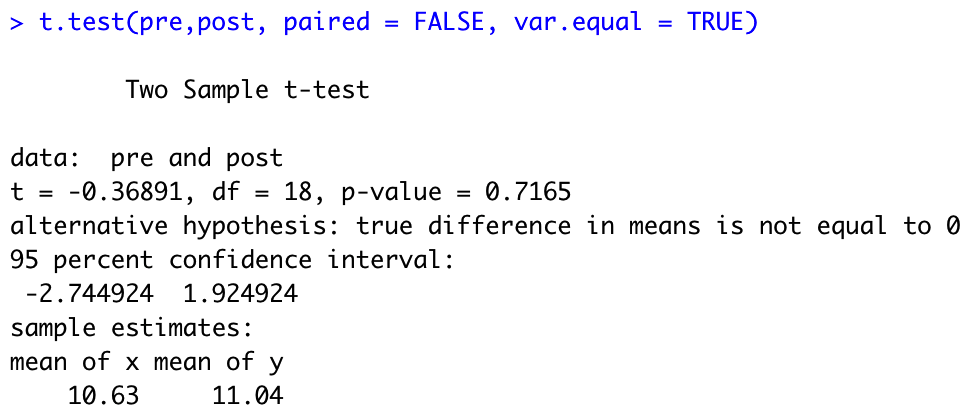
>> p-value가 0.05보다 크기 때문에 귀무가설을 채택한다.
[ pre와 post의 평균이 같다. ] (혈압약을 먹기 전과 후의 혈압이 같다.)
[ 사례 4 ] : 표본이 2개
# 두 개의 표본에 대한 평균이 같은지 검증
# 두 개의 모집단이 정규 분포하지 않는 경우의 검증 -> Wilcoxon rank sum test
질문 결과 A, B가 유의한 차이가 존재하는가?
| 5 | 4 | 3 | 2 | 1 | 합계 | |
| A | 8 | 11 | 9 | 2 | 3 | 33 |
| B | 4 | 6 | 10 | 8 | 4 | 32 |
A <- c(rep(5,8), rep(4, 11), rep(3,9), rep(2,2), rep(1,3))
B <- c(rep(5,4), rep(4, 6), rep(3, 10), rep(2,8), rep(1,4))
wilcox.test(A,B, exact = F, correct = F)
>> p-value가 0.05보다 작기 때문에 귀무가설을 기각하고 대립가설을 채택한다.
[ 유의한 차이가 존재한다. ]
'데이터분석 > R' 카테고리의 다른 글
| R - 비율검정 (0) | 2021.05.13 |
|---|---|
| R - [ 실습: 수면제 효과도 분석 ]: sleep 데이터 활용 (0) | 2021.05.13 |
| R - 난수, 분포함수 (0) | 2021.05.12 |
| R - welfare.csv, 결측치 대체 함수 작성 (0) | 2021.05.09 |
| R - Airquality (0) | 2021.05.09 |
